上一篇自然语言处理之LSA 介绍了LSA，本文介绍的PLSA(Probabilistic Latent Semantic Analysis, 概率潜在语义分析)由LSA发展而来。LSA使用线性代数方法，对document-word矩阵进行SVD分解。PLSA则使用了一个概率图模型，引入了一个隐变量topic（可以认为是文档的主题），然后进行统计推断。

为何提出PLSA

在语义分析问题中，存在同义词和一词多义这两个严峻的问题，LSA可以很好的解决同义词问题，却无法妥善处理一词多义问题。
PLSA则可以同时解决同义词和一词多义两个问题。

概率图模型

我们知道文档(一个句子、一个段落或一篇文章)都有它自己的主题，从大的方面讲有经济、政治、文化、体育、音乐、法律、动漫、游戏、法律等等主题，PLSA模型就引入了一个隐变量topic来表示这个主题。
PLSA的概率图模型如下图所示：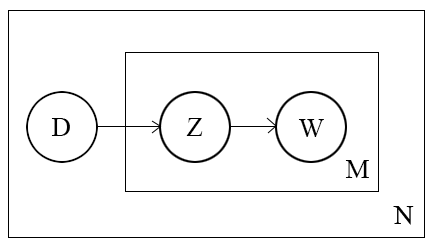

其中 $D$ 表示文档(document)，$Z$ 表示主题(topic), $W$ 表示单词(word)，其中箭头表示了变量间的依赖关系，比如 $D$ 指向 $Z$，表示一篇文档决定了该文档的主题，$Z$ 指向 $W$ 表示由该主题生成一个单词，方框右下角的字母表示该方框执行的次数，$N$ 表示共生成了 $N$ 篇文档，$M$ 表示一篇文档按照document-topic分布生成了 $M$ 次主题，每一次按照生成的主题的topic-word分布生成单词。每个文档的单词数可以不同。
PLSA引入了隐藏变量 $Z$，认为 $\lbrace{D,W,Z}\rbrace$ 表示完整的数据集(the complete data set), 而原始的真实数据集 $\lbrace{D,W}\rbrace$ 是不完整的数据集(incomplete data)。
假设 $Z$ 的取值共有 $K$ 个。PLSA模型假设的文档生成过程如下：

以 $p(d_i)$ 的概率选择一个文档 $d_i$
以 $p(z_k|d_i)$ 的概率选择一个主题 $z_k$
以 $p(w_j|z_k)$ 的概率生成一个单词 $w_j$
根据图模型，可以得到观测数据的联合分布：
$$
\begin{aligned}
p(d_i,w_j)&=\sum_{k=1}^{K}p(d_i,w_j,z_k) \\
&=\sum_{k=1}^{K}p(d_i)p(z_k|d_i)p(w_j|z_k) \\
&=p(d_i)\sum_{k=1}^{K}p(z_k|d_i)p(w_j|z_k)
\end{aligned}
$$
第一个等式是对三者的联合概率分布对其中的隐藏变量 $Z$ 的所有取值累加，第二个等式根据图模型的依赖关系将联合概率展开为条件概率，第三个等式只是简单的乘法结合律。这样就计算出了第 $i$ 篇文档与第 $j$ 个单词的联合概率分布。

complete-data log likelihood

我们可以得到完整数据的对数似然为：
$$
\begin{aligned}
L&=\sum_{i=1}^N\sum_{j=1}^{M}n(d_i,w_j)log(p(d_i,w_j)) \\
&=\sum_{i=1}^N\sum_{j=1}^{M}n(d_i,w_j)log(p(d_i)\sum_{k=1}^{K}p(z_k|d_i)p(w_j|z_k)) \\
&=\sum_{i=1}^{N}n(d_i)log(p(d_i))+\sum_{i=1}^N\sum_{j=1}^{M}n(d_i,w_j)log\sum_{k=1}^{K}p(z_k|d_i)p(w_j|z_k)
\end{aligned}
$$
其中 $n(d_i,w_j)$ 表示第 $j$ 个word在第 $i$ 个document中出现的次数。
上式左边一项对于给定的数据集来说是定值，我们只需要使得右边一项取到最大。
$p(z_k|d_i)$ 和 $p(w_j|z_k)$ 是PLSA模型需要求解的参数，按照通常的方法，可以通过对参数求导使用梯度下降或牛顿法等方法来求解，但是这里的参数以求和的形式出现在了对数函数之中，求导结果十分复杂，无法使用那些方法。
那么应该如何求解呢？答案是使用EM算法。

EM算法

这里，我们没有办法直接优化似然性 $L$, 而是通过找到一个辅助函数 $Q$, 使得每次增大辅助函数 $Q$ 的时候确保 $L$ 也能得到增加，图示如下：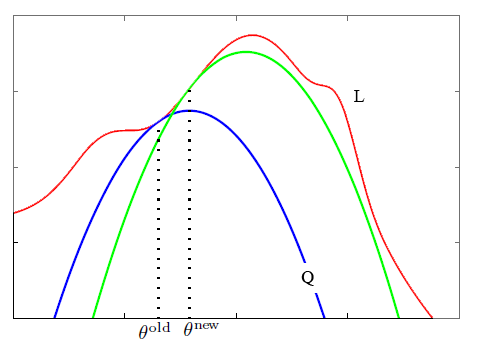

其中红线表示参数的似然性 $L$, 蓝线表示辅助函数 $Q$。
EM算法是一个迭代的过程，分为E步和M步，当未收敛或截断之前，重复执行E-Step和M-Step。
这里先给出EM算法辅助函数 $Q$ 的一般形式：
$$
Q(\theta,\theta^{old})=\sum_{z}p(z|x,\theta_{old})log(p(x,z;\theta))
$$
这个$Q$函数的物理意义是完整数据对数似然的期望，上式中 $x$和$z$的组合即为完整数据，对于每个隐含变量 $z$ 的取值，将这个完整数据的对数似然乘上隐含变量的后验概率，最后求和就是完整数据对数似然的期望(expectation of the complete-data log likelihood)。
在E-Step，根据一组旧的参数 $\theta^{old}$ 计算出隐含变量 $z$ 的后验概率，也就确定了一个参数 $\theta$ 的函数 $Q$, 比如这一轮E-Step得到了蓝线表示的$Q$。
然后在M-Step，可以计算出对应于蓝线 $Q$ 函数取得最大值对应的参数 $\theta^{new}$。从而在下一个E-Step得到一个新的 $Q$ 函数（绿线表示）。
可以在图中直观的看到似然性 $L$ 也同时得到了增加。
那么可能有人会产生这样的问题，凭什么 $L$ 难以直接优化，$Q$ 就容易优化，其实这是因为在 $Q$ 中的对数函数中不存在参数的和的形式，而 $L$ 中却存在。

使用EM求解PLSA

上面给出了EM算法 $Q$ 的一般形式，现在给出PLSA中 $Q$ 函数的形式：
$$
\begin{aligned}
Q(\theta,\theta^{old})&=\sum_{i=1}^N\sum_{j=1}^{M}n(d_i,w_j)\sum_{k=1}^{K}p(z_k|d_i,w_j)logp(d_i,w_j,z_k;\theta) \\
&=\sum_{i=1}^N\sum_{j=1}^{M}n(d_i,w_j)\sum_{k=1}^{K}p(z_k|d_i,w_j)log[p(d_i)p(z_k|d_i)p(w_j|z_k)]
\end{aligned}
$$
注意到这是因为如前文所说，在本问题中，认为$\lbrace{D,W,Z}\rbrace$ 是完整的数据集。
由于 $p(d_i)\propto{n(d_i)}$ ，$n(d_i)$ 表示第 $i$ 篇文档的单词总数，这一项估计并不重要，因此上式去掉该项，得到：
$$
Q(\theta,\theta^{old})=\sum_{i=1}^N\sum_{j=1}^{M}n(d_i,w_j)\sum_{k=1}^{K}p(z_k|d_i,w_j)log[p(z_k|d_i)p(w_j|z_k)]
$$
可以看到对数中是参数的乘积，不再包含求和的部分。
我们注意到，参数存在下面的两个约束:
$$
\sum_{j=1}^{M}p(w_j|z_k)=1
$$
$$
\sum_{k=1}^{K}p(z_k|d_i)=1
$$
因此可以使用拉格朗日乘子法(Lagrange multiplier)求取使得 $Q$ 函数最大时对应的参数。
写出拉格朗日函数:
$$
Lagrange=Q+\sum_{k=1}^{K}\tau_k(1-\sum_{j=1}^{M}p(w_j|z_k))+\sum_{i=1}^N\rho_i(1-\sum_{k=1}^{K}p(z_k|d_i))
$$
对拉格朗日函数中的 $p(w_j|z_k)$ 求偏导，令其等于零，得到：
$$
\sum_{i=1}^{N}n(d_i,w_j)p(z_k|d_i,w_j)-\tau_{k}p(w_j|z_k)=0, 1\leq{j}\leq{M},1\leq{k}\leq{K}
$$
对该式 $1\leq{j}\leq{M}$ 所有取值下等式两边累加，可以消去 $p(w_j|z_k)$, 从而得到 $\tau_{k}$ 的表达式，回带到上式得到下式：
$$
p(w_j|z_k)=\frac{\sum_{i=1}^{N}n(d_i,w_j)p(z_k|d_i,w_j)}{\sum_{l=1}^{M}\sum_{i=1}^{N}n(d_i,w_l)p(z_k|d_i,w_l)}
$$
对拉格朗日函数中的 $p(z_k|d_i)$ 求偏导，令其等于零，得到：
$$
\sum_{j=1}^{M}n(d_i,w_j)p(z_k|d_i,w_j)-\rho_{i}p(z_k|d_i)=0, 1\leq{i}\leq{N},1\leq{k}\leq{K}
$$
对该式 $1\leq{k}\leq{K}$ 所有取值下等式两边累加，可以消去 $p(z_k|d_i)$, 从而得到 $\rho_i$ 的表达式，回带到上式得到下式：
$$
p(z_k|d_i)=\frac{\sum_{j=1}^{M}n(d_i,w_j)p(z_k|d_i,w_j)}{n(d_i)}
$$
这样就得到了EM算法的M-Step重新估计参数的公式。
那么在E-Step如何计算 $z$ 的后验概率呢？根据下式计算，第一个等式是贝叶斯法则，第二个等式是根据图模型将联合概率展开，第三个等式是分子分母同时除以一个因子。
$$
\begin{aligned}
p(z_k|d_i,w_j)&=\frac{p(d_i,w_j,z_k)}{p(d_i,w_j)} \\
&=\frac{p(d_i)p(z_k|d_i)p(w_j|z_k)}{\sum_{l=1}^{K}p(d_i)p(z_l|d_i)p(w_j|z_l)} \\
&=\frac{p(z_k|d_i)p(w_j|z_k)}{\sum_{l=1}^{K}p(z_l|d_i)p(w_j|z_l)}
\end{aligned}
$$
那么何时停止算法呢？一种方法是计算完整数据的对数似然，当这个值的变化小于某个阈值时认为已经收敛；另一种方法可以固定迭代次数，进行截断，避免过拟合。

具体实现

代码中使用 $lamda[i,k]$表示参数 $p(z_k|d_i)$, 用 $theta[k,j]$ 表示参数 $p(w_j|z_k)$, 用 $p[i,j,k]$ 表示隐藏变量的后验概率 $p(z_k|d_i,w_j)$。
参数 $\theta$ 和 $\lambda$ 起初使用随机值初始化并归一化到和为1。
python代码如下。这里省略了导包语句、命令行读参语句、输出结果语句，完整代码见文末给出的github链接。

# segmentation, stopwords filtering and document-word matrix generating
# [return]:
# N : number of documents
# M : length of dictionary
# word2id : a map mapping terms to their corresponding ids
# id2word : a map mapping ids to terms
# X : document-word matrix, N*M, each line is the number of terms that show up in the document
def preprocessing(datasetFilePath, stopwordsFilePath):
    
    # read the stopwords file
    file = codecs.open(stopwordsFilePath, 'r', 'utf-8')
    stopwords = [line.strip() for line in file] 
    file.close()
    
    # read the documents
    file = codecs.open(datasetFilePath, 'r', 'utf-8')
    documents = [document.strip() for document in file] 
    file.close()

    # number of documents
    N = len(documents)

    wordCounts = [];
    word2id = {}
    id2word = {}
    currentId = 0;
    # generate the word2id and id2word maps and count the number of times of words showing up in documents
    for document in documents:
        segList = jieba.cut(document)
        wordCount = {}
        for word in segList:
            word = word.lower().strip()
            if len(word) > 1 and not re.search('[0-9]', word) and word not in stopwords:               
                if word not in word2id.keys():
                    word2id[word] = currentId;
                    id2word[currentId] = word;
                    currentId += 1;
                if word in wordCount:
                    wordCount[word] += 1
                else:
                    wordCount[word] = 1
        wordCounts.append(wordCount);
    
    # length of dictionary
    M = len(word2id)  

    # generate the document-word matrix
    X = zeros([N, M], int8)
    for word in word2id.keys():
        j = word2id[word]
        for i in range(0, N):
            if word in wordCounts[i]:
                X[i, j] = wordCounts[i][word];    

    return N, M, word2id, id2word, X

def initializeParameters():
    for i in range(0, N):
        normalization = sum(lamda[i, :])
        for j in range(0, K):
            lamda[i, j] /= normalization;

    for i in range(0, K):
        normalization = sum(theta[i, :])
        for j in range(0, M):
            theta[i, j] /= normalization;

def EStep():
    for i in range(0, N):
        for j in range(0, M):
            denominator = 0;
            for k in range(0, K):
                p[i, j, k] = theta[k, j] * lamda[i, k];
                denominator += p[i, j, k];
            if denominator == 0:
                for k in range(0, K):
                    p[i, j, k] = 0;
            else:
                for k in range(0, K):
                    p[i, j, k] /= denominator;

def MStep():
    # update theta
    for k in range(0, K):
        denominator = 0
        for j in range(0, M):
            theta[k, j] = 0
            for i in range(0, N):
                theta[k, j] += X[i, j] * p[i, j, k]
            denominator += theta[k, j]
        if denominator == 0:
            for j in range(0, M):
                theta[k, j] = 1.0 / M
        else:
            for j in range(0, M):
                theta[k, j] /= denominator
        
    # update lamda
    for i in range(0, N):
        for k in range(0, K):
            lamda[i, k] = 0
            denominator = 0
            for j in range(0, M):
                lamda[i, k] += X[i, j] * p[i, j, k]
                denominator += X[i, j];
            if denominator == 0:
                lamda[i, k] = 1.0 / K
            else:
                lamda[i, k] /= denominator

# calculate the log likelihood
def LogLikelihood():
    loglikelihood = 0
    for i in range(0, N):
        for j in range(0, M):
            tmp = 0
            for k in range(0, K):
                tmp += theta[k, j] * lamda[i, k]
            if tmp > 0:
                loglikelihood += X[i, j] * log(tmp)
    return loglikelihood
    
# set the default params
datasetFilePath = 'dataset.txt'
stopwordsFilePath = 'stopwords.dic'
K = 10    # number of topic
maxIteration = 30
threshold = 10.0
topicWordsNum = 10

# preprocessing
N, M, word2id, id2word, X = preprocessing(datasetFilePath, stopwordsFilePath)

# lamda[i, j] : p(zj|di)
lamda = random([N, K])

# theta[i, j] : p(wj|zi)
theta = random([K, M])

# p[i, j, k] : p(zk|di,wj)
p = zeros([N, M, K])

initializeParameters()

# EM algorithm
oldLoglikelihood = 1
newLoglikelihood = 1
for i in range(0, maxIteration):
    EStep()
    MStep()
    newLoglikelihood = LogLikelihood()
    print("[", time.strftime('%Y-%m-%d %H:%M:%S',time.localtime(time.time())), "] ", i+1, " iteration  ", str(newLoglikelihood))
    if(oldLoglikelihood != 1 and newLoglikelihood - oldLoglikelihood < convengenceThreshold):
        break
    oldLoglikelihood = newLoglikelihood

实验结果

Sample 1(English)

第一个实验使用从wikipedia获取的16个关于one piece的文档。
抽取出的10个topic的top 10单词结果如下。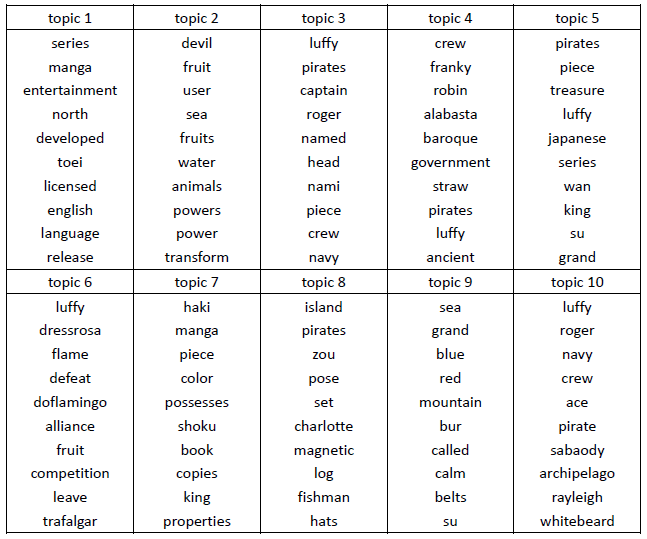

Sample 2(English)

第二个实验使用从Associated Press获取的100个新闻文档。
抽取出的10个topic的top 10单词结果如下。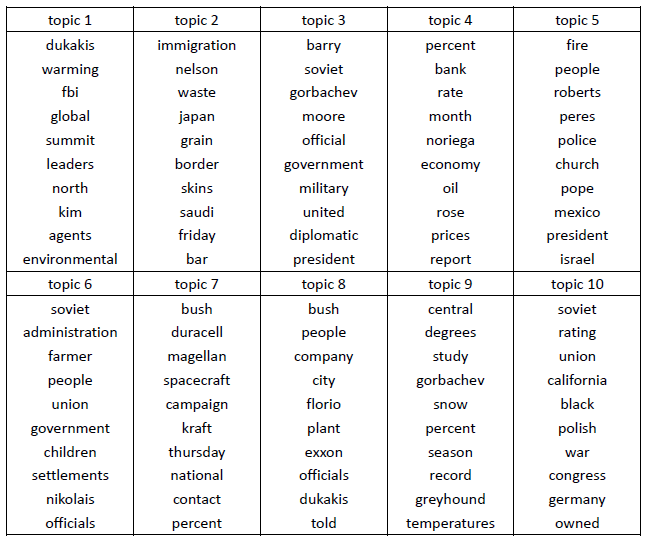

Sample 3(Chinese)

第三个实验使用从新浪获取的50篇社会新闻。
抽取出的30个topic的top 10单词结果如下。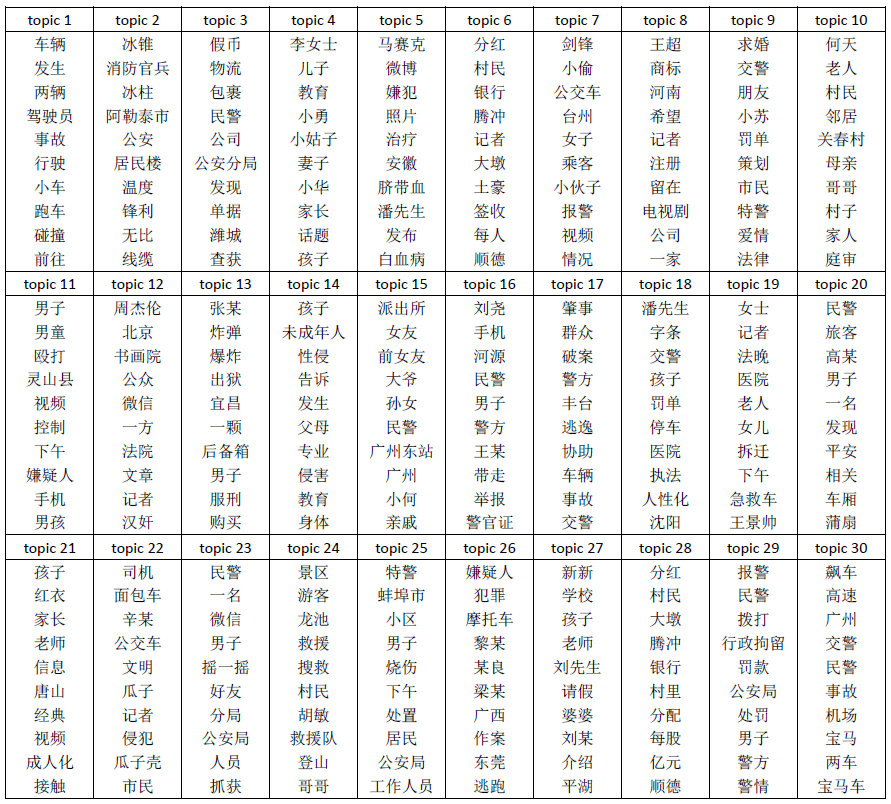

参考资料

1 Unsupervised Learning by Probabilistic Latent Semantic Analysis by Thomas Hofmann
2 Pattern Recognition and Machine Learning Chapter 9
3 wikipedia Lagrange multiplier

github项目

完整的代码、三个样例数据集、停用词表以及更多详情见我的github项目PLSA。
github项目链接