在上一篇 机器学习之线性回归 介绍了使用公式求解和批梯度下降两种方法进行线性回归模型的建立。本文将实现批梯度下降(batch gradient descent)以及随机梯度下降(stochastic gradient descent) 两种方法对线性回归问题建模并对比这两种方法。
回顾一下上篇使用的例子
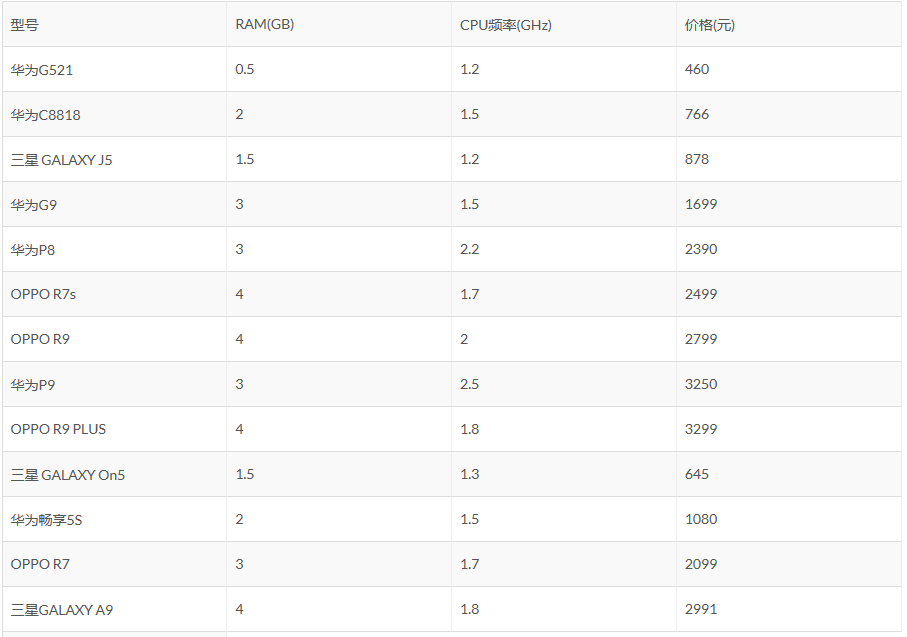
上表是一些手机价格的数据,我们用RAM和CPU频率作为特征,学得一个线性模型,来预测只给定RAM和CPU频率的新的手机的价格。使用前9条数据作为训练集,后4条数据作为测试集。
再谈批梯度下降
我们定义了损失函数:
$$
J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})^2
$$
对参数进行求导可得:
$$
\frac{\partial}{\partial\theta_j}J(\theta)=\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}
$$
上一篇已经实现了批梯度下降,不过参数更新以矩阵运算形式给出。只要收敛的阈值以及学习率设置的合理,批梯度下降是一定能够随着收敛阈值的减小而越接近于公式求解的结果的。
上一篇中给出的关键代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16load data; %导入X,Y,test_feature
epsilon = 0.0001; %收敛阈值
alpha = 0.0005; %学习率
theta = zeros(size(X,2),1);
k = 1; %迭代次数
while 1
J(k) = 1/2 * (norm(X*theta - Y))^2;
theta_new = theta - alpha*(X'*X*theta - X'*Y); %参数更新公式
if norm(theta_new-theta) < epsilon
theta = theta_new;
break;
else
theta = theta_new;
k = k + 1;
end
end
为了使用对损失函数的求导结果更加直观的表示出对每个参数的更新过程,我对其进行了如下改写:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24load data; %导入X,Y,test_feature
epsilon = 0.0001; %收敛阈值
alpha = 0.0005; %学习率
theta = zeros(size(X,2),1);
k = 1; %迭代次数
n = size(X,2); %特征数+1
m = size(X,1); %训练样本个数
theta_new = zeros(n,1);
while 1
J(k) = 1/2 * (norm(X*theta - Y))^2;
for(j = 1:n)
theta_new(j) = theta(j);
for(i = 1:m)
theta_new(j)=theta_new(j)-alpha*(X(i,:)*theta-Y(i,:))*X(i,j);
end;
end;
if norm(theta_new-theta) < epsilon
theta = theta_new;
break;
else
theta = theta_new;
k = k + 1;
end
end;
这一次我们可以清晰的看到,每一次参数的迭代更新,需要遍历全部的 $m$ 个训练样本,在我们的这个例子中 $m=9$ ,不会带来什么问题。
但我们试想若这个 $m$ 增大到在百万数量级以上,那么批梯度下降的效率是不是会大大的降低了呢?为解决此问题,我们将使用随机梯度下降。
随机梯度下降
不像批梯度下降每一次迭代,都要遍历全部的 $m$ 个样本。随机梯度下降每次迭代使用一个样本对参数进行更新,对全部样本循环使用。通常情况下,随机梯度下降得到一个离最小值较近的点的速度要比批梯度下降快得多,但如果学习率设置“过大”,有可能会导致 $J(\theta)$ 在最小值的附近反复震荡而无法收敛(可以考虑随着算法执行下调学习率以最终获得一个局部最优)。下面给出代码。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25load data; %导入X,Y,test_feature
epsilon = 0.0001; %收敛阈值
alpha = 0.001; %学习率
k = 1; %迭代次数
n = size(X,2); %特征数+1
m = size(X,1); %训练样本个数
theta = zeros(n,1);
theta_new = zeros(n,1);
converge = 0;
while(converge==0) %未收敛
for(i=1:m) %反复使用m个训练样本,每个样本就更新一次参数
J(k) = 1/2 * (norm(X*theta - Y))^2;
for(j = 1:n)
theta_new(j) = theta(j)-alpha*(X(i,:)*theta-Y(i,:))*X(i,j);
end;
if norm(theta_new-theta) < epsilon
converge=1;
theta = theta_new;
break;
else
theta = theta_new;
k = k + 1;
end
end;
end;
在本实验中,随机梯度下降的结果与直接用公式计算的结果对比如下图(带direct后缀为用公式计算)。

可以看到与公式计算的结果是有差距的,不过仍不失为一个不错的近似结果。随机梯度下降对于有巨大训练样本的问题意义重大。
线性回归的几种建模方法适用场景总结
1 公式求解
求解精准,适用于特征维度n不是特别大的问题,时间复杂度$O((n+1)^3)$。
2 批梯度下降
求解较准确,适用于训练样本总数m不是特别大的问题,可以解决1的问题。
3 随机梯度下降
求解是一个较好的估计值,可以解决1和2的问题。
参考资料
1 斯坦福机器学习公开课及其课程笔记 by Andrew Ng