android黑白棋游戏实现

发布于   |   分类于   |     |   阅读次数

黑白棋

黑白棋，又叫苹果棋，最早流行于西方国家。游戏通过相互翻转对方的棋子，最后以棋盘上谁的棋子多来判断胜负。黑白棋非常易于上手，但精通则需要考虑许多因素，比如角边这样的特殊位置、稳定度、行动力等。本游戏取名为黑白棋大师，提供了8种难度等级的选择，从菜鸟、新手、入门、棋手到棋士、大师、宗师、棋圣，助你不断提升棋力。
本文将着重介绍黑白棋实现过程中用到的算法。

黑白棋游戏规则

游戏规则见黑白棋大师中的截图。
rule

黑白棋大师游戏截图

游戏启动界面。
黑白棋游戏
游戏过程中的一个截图。
黑白棋游戏
开新局时的选项，选择先后手以及AI的水平。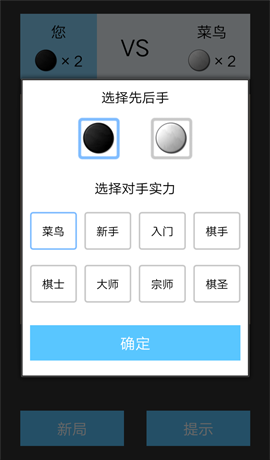
黑白棋游戏

几个关键的类

Rule

Rule类实现游戏规则相关的方法，包括

  1. 判断某一步是否合法
  2. 获取所有的合法走步
  3. 走一步并翻转敌方棋子
  4. 统计两方棋子个数

Algorithm

Algorithm类实现极小极大算法，包括

  1. 局面评估函数，对当前局面打分，越高对max越有利，越低对min越有利
  2. min()方法
  3. max()方法
  4. 获得一个好的走步

ReversiView

ReversiView继承自SurfaceView，实现棋盘的界面，在该类定义棋盘界面的绘制、更新等操作。

RenderThread

RenderThread继承自Thread，是控制ReversiView以一定fps更新、重绘界面的线程。

具体实现

棋盘表示

byte[][]二维数组存储棋盘，-1表示有黑子，1表示有白子，0表示棋格为空

游戏规则类Rule的实现

提供几个关于游戏规则的静态方法。

判断某一个位置是否位于棋盘内

1
2
3
public static boolean isLegal(int row, int col) {
    return row >= 0 && row < 8 && col >= 0 && col < 8;
}

判断某一方在某个位置落子是否合法

即判断该子是否能与己方棋子在某个方向上夹住敌方棋子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public static boolean isLegalMove(byte[][] chessBoard, Move move, byte chessColor) {
        int i, j, dirx, diry, row = move.row, col = move.col;
        if (!isLegal(row, col) || chessBoard[row][col] != Constant.NULL)
            return false;
        for (dirx = -1; dirx < 2; dirx++) {
            for (diry = -1; diry < 2; diry++) {
                if (dirx == 0 && diry == 0) continue;
                int x = col + dirx, y = row + diry;
                if (isLegal(y, x) && chessBoard[y][x] == (-chessColor)) {
                    for (i = row + diry * 2, j = col + dirx * 2; isLegal(i, j); i += diry, j += dirx) {
                        if (chessBoard[i][j] == (-chessColor)) {
                            continue;
                        } else if (chessBoard[i][j] == chessColor) {
                            return true;
                        } else {
                            break;
                        }
                    }
                }
            }
        }
        return false;
}

某一方走一步子

将各个方向上被翻转的棋子的颜色改变，并返回这些棋子在棋盘的位置，方便显示翻转动画。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public static List<Move> move(byte[][] chessBoard, Move move, byte chessColor) {
    int row = move.row;
    int col = move.col;
    int i, j, temp, m, n, dirx, diry;
    List<Move> moves = new ArrayList<Move>();
    for (dirx = -1; dirx < 2; dirx++) {
        for (diry = -1; diry < 2; diry++) {
            if (dirx == 0 && diry == 0)
                continue;
            temp = 0;
            int x = col + dirx, y = row + diry;
            if (isLegal(y, x) && chessBoard[y][x] == (-chessColor)) {
                temp++;
                for (i = row + diry * 2, j = col + dirx * 2; isLegal(i, j); i += diry, j += dirx) {
                    if (chessBoard[i][j] == (-chessColor)) {
                        temp++;
                        continue;
                    } else if (chessBoard[i][j] == chessColor) {
                        for (m = row + diry, n = col + dirx; m <= row + temp && m >= row - temp && n <= col + temp
                                && n >= col - temp; m += diry, n += dirx) {
                            chessBoard[m][n] = chessColor;
                            moves.add(new Move(m, n));
                        }
                        break;
                    } else
                        break;
                }
            }
        }
    }
    chessBoard[row][col] = chessColor;
    return moves;
}

获取某一方当前全部合法的落子位置

1
2
3
4
5
6
7
8
9
10
11
12
13
public static List<Move> getLegalMoves(byte[][] chessBoard, byte chessColor) {
    List<Move> moves = new ArrayList<Move>();
    Move move = null;
    for (int row = 0; row < 8; row++) {
        for (int col = 0; col < 8; col++) {
            move = new Move(row, col);
            if (Rule.isLegalMove(chessBoard, move, chessColor)) {
                moves.add(move);
            }
        }
    }
    return moves;
}

统计玩家和AI的棋子个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static Statistic analyse(byte[][] chessBoard, byte playerColor) {

    int PLAYER = 0;
    int AI = 0;
    for (int i = 0; i < 8; i++) {
        for (int j = 0; j < 8; j++) {
            if (chessBoard[i][j] == playerColor)
                PLAYER += 1;
            else if (chessBoard[i][j] == (byte)-playerColor)
                AI += 1;
        }
    }
    return new Statistic(PLAYER, AI);
}

游戏算法类Algorithm的实现

极大过程和极小过程

这两个过程的函数形式为：

1
2
private static MinimaxResult max(byte[][] chessBoard, int depth, int alpha, int beta, byte chessColor, int difficulty);
private static MinimaxResult min(byte[][] chessBoard, int depth, int alpha, int beta, byte chessColor, int difficulty);

chessBoard为棋盘；depth为博弈树搜索深度；alpha和beta用于alpha-beta剪枝，在max方法中alpha不断更新为局面评分的较大值，在min方法中beta不断更新为局面评分的较小值，当alpha >= beta时就进行剪枝；chessColor表示棋子颜色；difficulty表示游戏难度，对应于不同的AI水平。
由于黑子先行，黑子总是调用max()方法，白子调用min()方法。
下面以极大过程为例。
如果深度为0，只要返回当前局面评分即可。如果双方均没有步可走，表示已经达到最终局面，返回该局面评分。如果仅单方无处可走，调用min递归即可。
正常情况下有步可走，遍历每个合法的走步，如果alpha大于等于beta，剪枝直接break，否则走步并递归。
best是当前max节点维护的一个最佳值，调用的min方法的alpha是取得alpha和best的较大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
private static MinimaxResult max(byte[][] chessBoard, int depth, int alpha, int beta, byte chessColor, int difficulty) {
    if (depth == 0) {
        return new MinimaxResult(evaluate(chessBoard, difficulty), null);
    }
    List<Move> legalMovesMe = Rule.getLegalMoves(chessBoard, chessColor);
    if (legalMovesMe.size() == 0) {
        if (Rule.getLegalMoves(chessBoard, (byte)-chessColor).size() == 0) {
            return new MinimaxResult(evaluate(chessBoard, difficulty), null);
        }
        return min(chessBoard, depth, alpha, beta, (byte)-chessColor, difficulty);
    }
    byte[][] tmp = new byte[8][8];
    Util.copyBinaryArray(chessBoard, tmp);
    int best = Integer.MIN_VALUE;
    Move move = null;

    for (int i = 0; i < legalMovesMe.size(); i++) {
        alpha = Math.max(best, alpha);
        if(alpha >= beta){
            break;
        }
        Rule.move(chessBoard, legalMovesMe.get(i), chessColor);
        int value = min(chessBoard, depth - 1, Math.max(best, alpha), beta, (byte)-chessColor, difficulty).mark;
        if (value > best) {
            best = value;
            move = legalMovesMe.get(i);
        }
        Util.copyBinaryArray(tmp, chessBoard);
    }
    return new MinimaxResult(best, move);
}

private static MinimaxResult min(byte[][] chessBoard, int depth, int alpha, int beta, byte chessColor, int difficulty) {
    if (depth == 0) {
        return new MinimaxResult(evaluate(chessBoard, difficulty), null);
    }
    List<Move> legalMovesMe = Rule.getLegalMoves(chessBoard, chessColor);
    if (legalMovesMe.size() == 0) {
        if (Rule.getLegalMoves(chessBoard, (byte)-chessColor).size() == 0) {
            return new MinimaxResult(evaluate(chessBoard, difficulty), null);
        }
        return max(chessBoard, depth, alpha, beta, (byte)-chessColor, difficulty);
    }
    byte[][] tmp = new byte[8][8];
    Util.copyBinaryArray(chessBoard, tmp);
    int best = Integer.MAX_VALUE;
    Move move = null;

    for (int i = 0; i < legalMovesMe.size(); i++) {
        beta = Math.min(best, beta);
        if(alpha >= beta){
            break;
        }
        Rule.move(chessBoard, legalMovesMe.get(i), chessColor);
        int value = max(chessBoard, depth - 1, alpha, Math.min(best, beta), (byte)-chessColor, difficulty).mark;
        if (value < best) {
            best = value;
            move = legalMovesMe.get(i);
        }
        Util.copyBinaryArray(tmp, chessBoard);
    }
    return new MinimaxResult(best, move);
}

alpha-beta剪枝原理

先解释下alpha和beta的物理含义，alpha表示max节点迄今为止的最佳局面评分，beta表示min节点迄今为止的最佳局面评分。
举个例子见下图（数值为虚构），假设深度是两层，每个结点有两行数字，上方的两个数分别是alpha和beta，表示作为参数传到该层的alpha和beta。下方的数表示了该节点best的更新过程。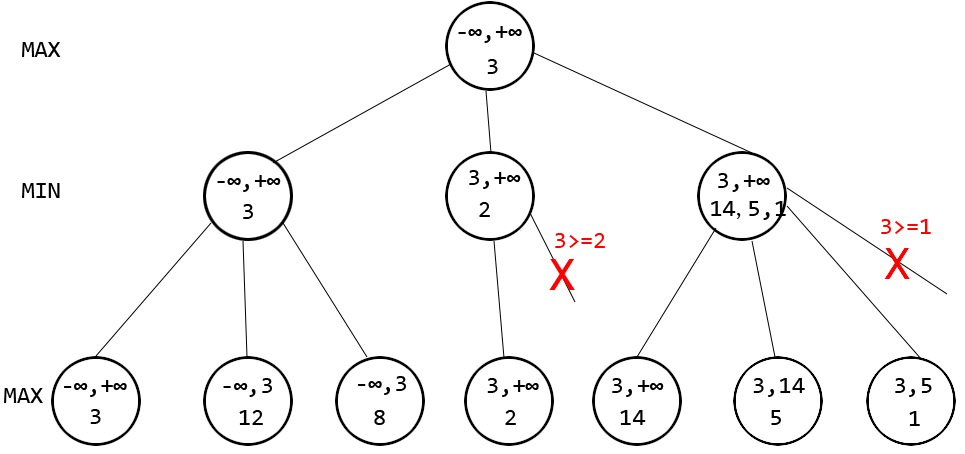
alpha-beta
看图中第一个红色的叉号，该位置处会更新beta为正无穷和2的较小值，即2，导致alpha大于等于beta成立，发生剪枝，对应于min方法中相应位置处的break操作。

获得AI计算出的最佳走步

该方法用于AI走步以及提示功能。

1
2
3
4
5
6
public static Move getGoodMove(byte[][] chessBoard, int depth, byte chessColor, int difficulty) {
        if (chessColor == Constant.BLACK)
            return max(chessBoard, depth, Integer.MIN_VALUE, Integer.MAX_VALUE, chessColor, difficulty).move;
        else
            return min(chessBoard, depth, Integer.MIN_VALUE, Integer.MAX_VALUE, chessColor, difficulty).move;
}

局面评估函数

局面评估函数决定了AI水平的高低。对应于不同的AI等级，设计了不同的评估函数。
菜鸟级别只关注棋子个数，新手、入门、棋手3个级别不仅关注棋子的个数，而且关注特殊位置的棋子（边、角），棋士和大师级别在棋子个数、边角之外还考虑了行动力，即对方下轮可选的下子位置的个数，宗师和棋圣考虑稳定度和行动力。稳定度将在下一小节介绍。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
private static int evaluate(byte[][] chessBoard, int difficulty) {
        int whiteEvaluate = 0;
        int blackEvaluate = 0;
        switch (difficulty) {
        case 1:
            for (int i = 0; i < 8; i++) {
                for (int j = 0; j < 8; j++) {
                    if (chessBoard[i][j] == WHITE) {
                        whiteEvaluate += 1;
                    } else if (chessBoard[i][j] == BLACK) {
                        blackEvaluate += 1;
                    }
                }
            }
            break;
        case 2:
        case 3:
        case 4:
            for (int i = 0; i < 8; i++) {
                for (int j = 0; j < 8; j++) {
                    if ((i == 0 || i == 7) && (j == 0 || j == 7)) {
                        if (chessBoard[i][j] == WHITE) {
                            whiteEvaluate += 5;
                        } else if (chessBoard[i][j] == BLACK) {
                            blackEvaluate += 5;
                        }
                    } else if (i == 0 || i == 7 || j == 0 || j == 7) {
                        if (chessBoard[i][j] == WHITE) {
                            whiteEvaluate += 2;
                        } else if (chessBoard[i][j] == BLACK) {
                            blackEvaluate += 2;
                        }
                    } else {
                        if (chessBoard[i][j] == WHITE) {
                            whiteEvaluate += 1;
                        } else if (chessBoard[i][j] == BLACK) {
                            blackEvaluate += 1;
                        }
                    }
                }
            }
            break;
        case 5:
        case 6:
            for (int i = 0; i < 8; i++) {
                for (int j = 0; j < 8; j++) {
                    if ((i == 0 || i == 7) && (j == 0 || j == 7)) {
                        if (chessBoard[i][j] == WHITE) {
                            whiteEvaluate += 5;
                        } else if (chessBoard[i][j] == BLACK) {
                            blackEvaluate += 5;
                        }
                    } else if (i == 0 || i == 7 || j == 0 || j == 7) {
                        if (chessBoard[i][j] == WHITE) {
                            whiteEvaluate += 2;
                        } else if (chessBoard[i][j] == BLACK) {
                            blackEvaluate += 2;
                        }
                    } else {
                        if (chessBoard[i][j] == WHITE) {
                            whiteEvaluate += 1;
                        } else if (chessBoard[i][j] == BLACK) {
                            blackEvaluate += 1;
                        }
                    }
                }
            }
            blackEvaluate = blackEvaluate * 2 + Rule.getLegalMoves(chessBoard, BLACK).size();
            whiteEvaluate = whiteEvaluate * 2 + Rule.getLegalMoves(chessBoard, WHITE).size();
            break;
        case 7:
        case 8:
            /**
             * 稳定度
             */
            for (int i = 0; i < 9; i++) {
                for (int j = 0; j < 9; j++) {
                    int weight[] = new int[] { 2, 4, 6, 10, 15 };
                    if (chessBoard[i][j] == WHITE) {
                        whiteEvaluate += weight[getStabilizationDegree(chessBoard, new Move(i, j))];
                    } else if (chessBoard[i][j] == BLACK) {
                        blackEvaluate += weight[getStabilizationDegree(chessBoard, new Move(i, j))];
                    }
                }
            }
            /**
             * 行动力
             */
            blackEvaluate += Rule.getLegalMoves(chessBoard, BLACK).size();
            whiteEvaluate += Rule.getLegalMoves(chessBoard, WHITE).size();
            break;
        }
        return blackEvaluate - whiteEvaluate;
}

稳定度计算

我们知道，在黑白棋中，棋盘四角的位置一旦占据是不可能再被翻转的，因此这几个位置上的子必然是稳定子，而边上的子只有可能沿边的方向被翻转，稳定的程度高于中间的位置上的子。
因此，试图给每个子定义一个稳定度，描述该子不被翻转的稳定程度。
一共有四个方向，即左-右，上-下，左上-右下，右上-左下。举个例子，下面代码中的 (drow[0][0], dcol[0][0])表示向左移动一个单位的向量，(drow[0][1], dcol[0][1])表示向右移动一个单位的向量。
对于棋盘中某个子的位置，向左找到第一个不是该颜色的位置（可以是出界），再向右找到第一个不是该颜色的位置（可以是出界），如果这两个位置至少有一个出界，或者两个均为敌方棋子，稳定度加1。
对于另外三个方向作同样操作。可以看到，角上的棋子的稳定度必然为4，其他位置则根据具体情况并不恒定不变。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
private static int getStabilizationDegree(byte[][] chessBoard, Move move) {
        int chessColor = chessBoard[move.row][move.col];
        int drow[][], dcol[][];
        int row[] = new int[2], col[] = new int[2];
        int degree = 0;

        drow = new int[][] { { 0, 0 }, { -1, 1 }, { -1, 1 }, { 1, -1 } };
        dcol = new int[][] { { -1, 1 }, { 0, 0 }, { -1, 1 }, { -1, 1 } };

        for (int k = 0; k < 4; k++) {
            row[0] = row[1] = move.row;
            col[0] = col[1] = move.col;
            for (int i = 0; i < 2; i++) {
                while (Rule.isLegal(row[i] + drow[k][i], col[i] + dcol[k][i])
                        && chessBoard[row[i] + drow[k][i]][col[i] + dcol[k][i]] == chessColor) {
                    row[i] += drow[k][i];
                    col[i] += dcol[k][i];
                }
            }
            if (!Rule.isLegal(row[0] + drow[k][0], col[0] + dcol[k][0])
                    || !Rule.isLegal(row[1] + drow[k][1], col[1] + dcol[k][1])) {
                degree += 1;
            } else if (chessBoard[row[0] + drow[k][0]][col[0] + dcol[k][0]] == (-chessColor)
                    && chessBoard[row[1] + drow[k][1]][col[1] + dcol[k][1]] == (-chessColor)) {
                degree += 1;
            }
        }
        return degree;
}

项目开源

完整项目已经开源到github上。
github项目主页: Reversi