LDA由PLSA发展而来,PLSA由LSA发展而来,同样用于隐含语义分析,这里先给出两篇实现LSA和PLSA的文章链接。
自然语言处理之LSA
自然语言处理之PLSA
我们知道,PLSA也定义了一个概率图模型,假设了数据的生成过程,但是不是一个完全的生成过程:没有给出先验。因此PLSA给出的是一个最大似然估计(ML)或者最大后验估计(MAP)。
LDA拓展了PLSA,定义了先验,因此LDA给出的是一个完整的贝叶斯估计。
符号
这里先给出本文公式中以及python代码中使用到的符号及其含义。关于编号,公式中从1开始编号,代码中从0开始编号,只是为了方便。
| 公式中的符号 | 描述 | 代码中的符号 | 描述 |
|---|---|---|---|
| $N$ | 文档总数 | N | |
| $N_i$ | 第i篇文档单词数 | ||
| $K$ | topic总数 | K | |
| $M$ | 词表长度 | M | |
| $d$ | 文档编号,是一个整数 | d | |
| $z$ | topic编号,是一个整数 | z | |
| $w$ | 单词编号,是一个整数 | w | |
| $\vec{\alpha}$ | document-topic分布的超参数,是一个K维向量 | alpha | 是一个标量,$\vec{\alpha}$的每一维都是alpha |
| $\vec{\beta}$ | topic-word分布的超参数,是一个M维向量 | beta | 是一个标量,$\vec{\beta}$的每一维都是beta |
| $\vec{\theta_i}$ | $p(z{\vert}d=i)$组成的K维向量,其中$z\in[1,K]$ | ||
| $\Theta$ | $\Theta=\lbrace\vec{\theta_i}\rbrace^{N}_{i=1}$ | ||
| $\vec{\varphi_k}$ | $p(w{\vert}z=k)$组成的M维向量,其中$w\in[1,M]$ | ||
| $\Phi$ | $\Phi=\lbrace\vec{\varphi_k}\rbrace^{K}_{k=1}$ | ||
| $z_{i,j}$ | 第i篇文档的第j个单词的topic编号 | Z[i,j] | Z是一个元素为list的list |
| $w_{i,j}$ | 第i篇文档的第j个单词在词表中的编号 | docs[i,j] | docs是一个元素为list的list |
| $l$ | 二维下标(i,j),对应第i篇文档的第j个单词 | ||
| $\urcorner{l}$ | 下标包含这一项表示将第i篇文档的第j个单词排除在外 | ||
| $n_{iz}$ | 第i篇文档中由z这个topic产生的单词计数 | ndz[i,z] | ndz是一个二维矩阵,ndz[i,z]等于$n_{iz}$加上伪计数alpha |
| $n_{i}$ | 第i篇文档由每个topic产生的单词计数组成的向量 | ||
| $n_{zw}$ | 第z个topic产生单词w的计数 | nzw[z,w] | nzw是一个二维矩阵,nzw[z,w]等于$n_{zw}$加上伪计数beta |
| $n_{z}$ | 第z个topic产生全部单词的计数 | nz[z] | nz是一个一维矩阵,nz[z]等于$n_{z}$加上M倍的beta |
概率图模型
LDA的概率图模型见下图。箭头定义了随机变量间的关系。每个方框定义了每个过程,方框右下角的变量是该过程的重复次数。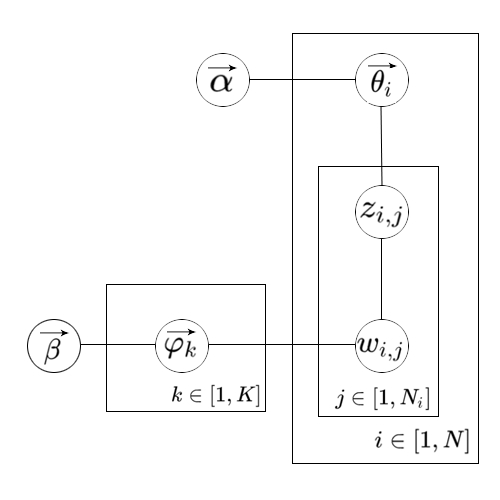
生成过程
LDA认为数据的生成过程如下图。
由该生成过程以及dirichlet-multinomial共轭可得:
$$
p(\vec{z}|\vec{\alpha})=\prod^{N}_{i=1}\frac{\Delta(\vec{n_i}+\vec{\alpha})}{\Delta(\vec{\alpha})}
$$
$$
p(\vec{w}|\vec{z},\vec{\beta})=\prod^{K}_{z=1}\frac{\Delta(\vec{n_z}+\vec{\beta})}{\Delta(\vec{\beta})}
$$
$$
\begin{aligned}
p(\vec{w},\vec{z}|\vec{\alpha},\vec{\beta})&=p(\vec{w}|\vec{z},\vec{\beta})p(\vec{z}|\vec{\alpha}) \\
&=\prod^{K}_{z=1}\frac{\Delta(\vec{n_z}+\vec{\beta})}{\Delta(\vec{\beta})}\prod^{N}_{i=1}\frac{\Delta(\vec{n_i}+\vec{\alpha})}{\Delta(\vec{\alpha})}
\end{aligned}
$$
从而得到了联合概率分布 $p(\vec{w},\vec{z})$。
似然性
根据上面的概率图模型,可以得出第i篇文档的complete-data似然性为:
$$
p(\vec{w_i},\vec{z_i},\vec{\theta_{i}},\Phi|\vec{\alpha},\vec{\beta})=\prod^{N_i}_{j=1}p(w_{i,j}|\vec{\varphi_{z_{i,j}}})p(z_{i,j}|\vec{\theta_i}){\cdot}p(\vec{\theta_i}|\vec{\alpha}){\cdot}p(\Phi|\vec{\beta})
$$
第i篇文档第j个单词在词表中编号为w的概率为:
$$
p(w_{i,j}=w|\vec{\theta_i},\Phi)=\sum^{K}_{k=1}p(w_{i,j}=w|\vec{\varphi_k})p(z_{i,j}=k|\vec{\theta_i})
$$
整个数据集的似然性为:
$$
p(\mathcal{D}|\Theta,\Phi)=\prod^{N}_{i=1}p(\vec{w_i}|\vec{\theta_i},\Phi)=\prod^{N}_{i=1}\prod^{N_i}_{j=1}p(w_{i,j}|\vec{\theta_i},\Phi)
$$
那么接下来怎么办呢?我们回忆一下在PLSA中是怎么做的。
PLSA中的概率图模型由于没有先验,模型比LDA简单一些,认为文档决定topic,topic决定单词,写出了整个数据集的对数似然性,然后由于要求解的参数以求和的形式出现在了对数函数中,无法通过直接求导使用梯度下降或牛顿法来使得这个对数似然最大,因此使用了EM算法。
LDA同样可以使用EM算法求解参数,但需要在E步计算隐变量的后验概率时使用变分推断进行近似,一种更简单的方法是使用gibbs sampling。
gibbs sampling
根据生成过程已经得到了联合概率分布 $p(\vec{w},\vec{z})$。由于每个文档中的单词 $\vec{w}$ 是可以观测到的已知数据,我们需要采样的分布是 $p(\vec{z}|\vec{w})$。
下面推导gibbs sampling采样 $p(\vec{z}|\vec{w})$ 分布的公式。
$$
\begin{aligned}
p(z_l=z|\vec{z_{\urcorner{l}}},\vec{w})&=\frac{p(\vec{w},\vec{z})}{p(\vec{w},\vec{z_{\urcorner{l}}})} \\
&=\frac{p(\vec{w}|\vec{z})p(\vec{z})}{p(\vec{w_{\urcorner{l}}}|\vec{z_{\urcorner{l}}})p(w_l)p(\vec{z_{\urcorner{l}}})} \\
&\propto{\frac{p(\vec{w}|\vec{z})p(\vec{z})}{p(\vec{w_{\urcorner{l}}}|\vec{z_{\urcorner{l}}})p(\vec{z_{\urcorner{l}}})}} \\
&=\frac{\Delta(\vec{n_i}+\vec{\alpha})}{\Delta(\vec{n_{i,\urcorner{l}}}+\vec{\alpha})}\cdot\frac{\Delta(\vec{n_z}+\vec{\beta})}{\Delta(\vec{n_{z,\urcorner{l}}}+\vec{\beta})} \\
&=\frac{\Gamma(n_{iz}+\alpha_{z})\Gamma(\sum^{K}_{z=1}(n_{iz,\urcorner{l}}+\alpha_{z}))}{\Gamma(n_{iz,\urcorner{l}}+\alpha_{z})\Gamma(\sum^{K}_{z=1}(n_{iz}+\alpha_{z}))}\cdot\frac{\Gamma(n_{zw}+\beta_{w})\Gamma(\sum^{M}_{w=1}(n_{zw,\urcorner{l}}+\beta_{w}))}{\Gamma(n_{zw,\urcorner{l}}+\beta_{w})\Gamma(\sum^{M}_{w=1}(n_{zw}+\beta_{w}))} \\
&=\frac{n_{iz,\urcorner{l}}+\alpha_{z}}{\sum^{K}_{z=1}(n_{iz,\urcorner{l}}+\alpha_{z})}\cdot\frac{n_{zw,\urcorner{l}}+\beta_{w}}{\sum^{M}_{w=1}(n_{zw,\urcorner{l}}+\beta_{w})} \\
&\propto{\frac{n_{zw,\urcorner{l}}+\beta_{w}}{\sum^{M}_{w=1}(n_{zw,\urcorner{l}}+\beta_{w})}\cdot(n_{iz,\urcorner{l}}+\alpha_{z})} \\
&=\frac{nzw[z,w]}{nz[z]}\cdot(ndz[i,z])
\end{aligned}
$$
下面解释一下这个推导过程,前两个等号是利用了贝叶斯公式,第三步的正比于符号这一行是去掉了一项常数 $p(w_l)$,第四步利用了前面计算好的 $p(\vec{w},\vec{z})$ 联合概率公式,第五、六步是将函数展开并化简,第七步的正比于符号是去掉了一项不依赖于z的项(即z取何值该项都相同),最后一行给出了对应代码中的表达。
这样我们就得到了吉布斯采样公式,每一轮gibbs sampling的迭代中依次遍历每个二维下标 $l$, 即遍历每篇文档的每一个单词,重新采样这个下标对应的topic编号。
LDA的实现
用python编写了一个使用gibbs sampling实现的LDA。数据集放在文件dataset.txt中,一行表示一篇文档,只需使用原始数据即可,可处理中文和英文。
采用了jieba分词工具,停止词使用英文停止词、中文停止词、标点符号以及所有日文字符。
下面给出代码。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98# 预处理(分词,去停用词,为每个word赋予一个编号,文档使用word编号的列表表示)
def preprocessing(filename):
# 读取停止词文件
file = codecs.open('stopwords.dic','r','utf-8')
stopwords = [line.strip() for line in file]
file.close()
# 读数据集
file = codecs.open('dataset.txt','r','utf-8')
documents = [document.strip() for document in file]
file.close()
word2id = {}
id2word = {}
docs = []
currentDocument = []
currentWordId = 0
for document in documents:
# 分词
segList = jieba.cut(document)
for word in segList:
word = word.lower().strip()
# 单词长度大于1并且不包含数字并且不是停止词
if len(word) > 1 and not re.search('[0-9]', word) and word not in stopwords:
if word in word2id:
currentDocument.append(word2id[word])
else:
currentDocument.append(currentWordId)
word2id[word] = currentWordId
id2word[currentWordId] = word
currentWordId += 1
docs.append(currentDocument);
currentDocument = []
return docs, word2id, id2word
# 初始化,按照每个topic概率都相等的multinomial分布采样,等价于取随机数,并更新采样出的topic的相关计数
def randomInitialize():
for d, doc in enumerate(docs):
zCurrentDoc = []
for w in doc:
pz = np.divide(np.multiply(ndz[d, :], nzw[:, w]), nz)
z = np.random.multinomial(1, pz / pz.sum()).argmax()
zCurrentDoc.append(z)
ndz[d, z] += 1
nzw[z, w] += 1
nz[z] += 1
Z.append(zCurrentDoc)
# gibbs采样
def gibbsSampling():
# 为每个文档中的每个单词重新采样topic
for d, doc in enumerate(docs):
for index, w in enumerate(doc):
z = Z[d][index]
# 将当前文档当前单词原topic相关计数减去1
ndz[d, z] -= 1
nzw[z, w] -= 1
nz[z] -= 1
# 重新计算当前文档当前单词属于每个topic的概率
pz = np.divide(np.multiply(ndz[d, :], nzw[:, w]), nz)
# 按照计算出的分布进行采样
z = np.random.multinomial(1, pz / pz.sum()).argmax()
Z[d][index] = z
# 将当前文档当前单词新采样的topic相关计数加上1
ndz[d, z] += 1
nzw[z, w] += 1
nz[z] += 1
alpha = 5
beta = 0.1
iterationNum = 50
K = 10
# 预处理
docs, word2id, id2word = preprocessing("data.txt")
Z = []
N = len(docs)
M = len(word2id)
# ndz[d,z]表示文档d中由topic z产生的单词计数加伪计数alpha
ndz = np.zeros([N, K]) + alpha
# nzw[z,w]表示topic z产生的单词w的计数加伪计数beta
nzw = np.zeros([K, M]) + beta
# nz[z]表示topic z产生的所有单词的总计数加伪计数
nz = np.zeros([K]) + M * beta
# 初始化
randomInitialize()
# gibbs sampling
for i in range(0, iterationNum):
gibbsSampling()
# 产生每个topic的top10的词
topicwords = []
maxTopicWordsNum = 10
for z in range(0, K):
ids = nzw[z, :].argsort()
topicword = []
for j in ids:
topicword.insert(0, id2word[j])
topicwords.append(topicword[0 : min(10, len(topicword))])
实验结果
实验部分,使用两个数据集进行测试,第一个数据集是PLSA实验中使用的第二个关于one piece的16个英文文档,来源于维基百科,其中包含日文字符,因此停止词中加入了日语字符,第二个数据集是5000篇新浪社会新闻,是中文文档。
第一个英文数据集的部分截图如下。
设置的参数为K=10,iterationNum=50。
实验结果如下图。给出了每个主题top10的词语。
第二个中文数据集的部分截图如下。
参数设置为K=10,iterationNum=50:
主题0关于犯罪,主题8关于法院,主题2关于医疗,主题3关于交通事故,主题4关于学校,主题7是一些称谓,主题6关于社区。
参数设置为K=30,iterationNum=50: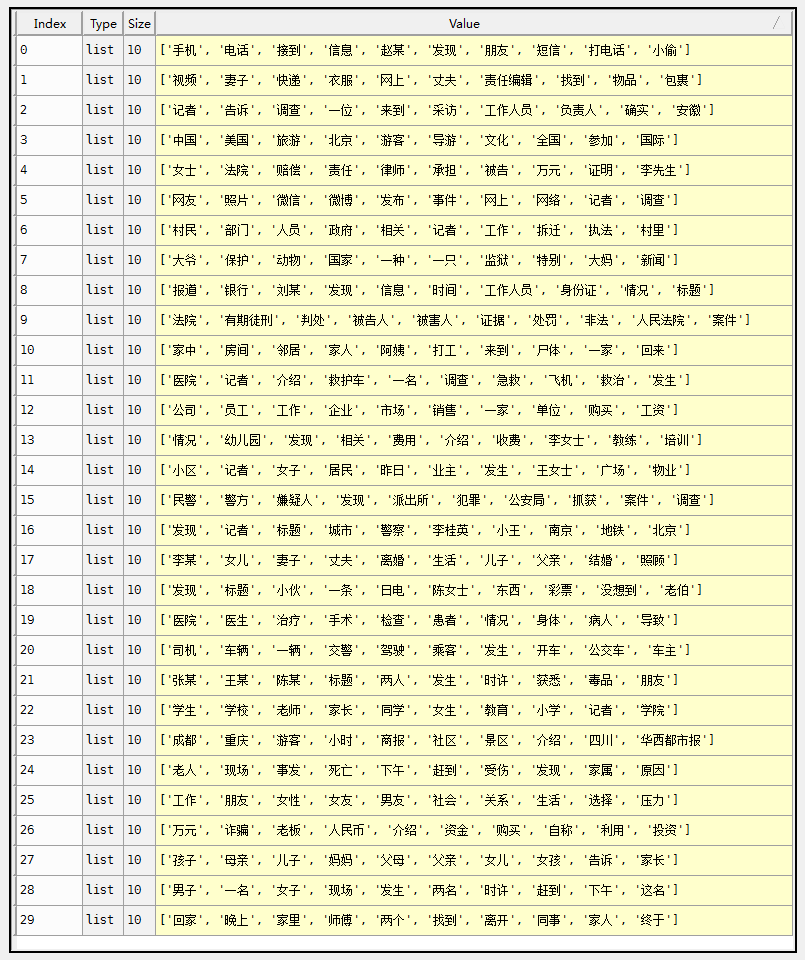
可以看到,当topic数设置大一些,得到的主题将变得更为具体一些。由于停止词表的选用问题,有些停止词没有被过滤掉,比如一种,一只等数量词,完善停止词表可以让结果更好。
参考资料
1 Parameter estimation for text analysis by Gregor Heinrich
2 Latent Dirichlet Allocation by David M. Blei et al.
3 LDA数学八卦 by Rickjin
完整代码、停用词以及数据集已托管至 github