机器学习之感知机

发布于   |   分类于   |     |   阅读次数

什么是感知机

感知机（perceptron）是一种二类分类的线性分类模型。假设特征空间是 χ⊆Rn , 输出空间是 Υ={+1,−1} , 输入 x∈χ 表示特征向量，输出 y∈Υ 表示类别。由输入空间到输出空间的如下函数称为感知机：
f(x)=sign(wx+b)

其中，w 和 b 是感知机模型参数，上式 wx 表示两个向量的点乘，sign是符号函数：
sign(x)={+1,x≥0−1,x<0

感知机的几何解释

线性方程 wx+b=0 对应于特征空间 Rn 中的一个超平面 S，其中 w 是超平面的法向量, b 是超平面的截距。这个超平面将特征空间划分为两个部分。位于两部分的点（特征向量）分别被分为正、负两类。因此，超平面 S 被称为分离超平面。
感知机的目标就是学习参数 w 和 b ，找到一个能够将训练集中的正样本与负样本完全正确分开的分离超平面，然后根据这些参数对新来的测试样本进行预测，得到其类别（我们假设数据集是线性可分的）。

如何实现

感知机定义的损失函数是误分类点到超平面 S 的总距离，输入空间 Rn 中任一点 x0 到超平面 S 的距离是：
1∣∣w∣∣∣wx0+b∣

这里，∣∣w∣∣ 是 w 的L2范数，对于分类错误的样本 (xi,yi) 来说，我们有下式成立：
−yi(wxi+b)>0

因此，分类错误的样本点 xi 到超平面 S 的距离可以写为：
L=−1∣∣w∣∣yi(wxi+b)

这里可以很容易的对参数 w 和 b 求偏导，得到：
∂∂wL=−1∣∣w∣∣yixi


∂∂bL=−1∣∣w∣∣yi

这样我们就得到了使用随机梯度下降法来学习参数 w 和 b 时的更新参数的公式了。
在此，我们用W0 来表示 b , W 表示增广矩阵 [b;w] (w是列向量)，同时定义 x0=1 。
那么上面的 wx+b 可以写为 WTx , 求导公式可以统一为：
∂∂WL=−1∣∣w∣∣yixi

我们可以写出参数的更新公式如下式：
W=W+αyixi;

其中 α 是学习率，可以看到更新公式忽略掉了求导公式中的前面的系数，并加上了一个学习率参数。
这是因为那个系数只会改变大小，而不会改变正负。
这样，我们就可以每次对于一个分类错误的样本，使其梯度下降，最终能够收敛（前提是数据集线性可分）是可以得到证明的。这里不提。

具体实现

以一个简单的例子来实现一个感知机模型。
三个训练样本的特征分别为(3,3), (4,3), (1,1), 对应的类别分别是+1, +1, -1。现在要实现一个感知机,并预测两个测试样本(-1,1),(6,2)的类别。
先给出matlab代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
load data;
X = [ones(size(train_feature,1),1) train_feature]; %增加一列1，表示增广的特征
n = size(X,2); %特征数+1
m = size(X,1); %样本数
Y = train_label; %真实类别
W = zeros(n,1);  %增广的权重向量，初始全为0
alpha = 1;   %学习率
count = 0;  %连续正确分类的样本记数
converge = 0; %是否已经收敛
while converge == 0
    for i=1:m
        % 当前训练样本分类错误，更新参数
        if Y(i)*(W'*X(i,:)') <= 0
            W = W + alpha*Y(i)*X(i,:)';
            count = 0;
        else
            count = count + 1;
            if count == m
                converge = 1;
                break;
            end;
        end;
    end;
end;
% 测试样本的特征也增加一列1
test_feature = [ones(size(test_feature,1),1) test_feature];
% 进行预测
predict = sign(W'*test_feature')';

其中X的每一行表示一个训练样本的特征向量。
可以看到，当全部样本都预测正确时认为算法收敛，只要判断连续的正确分类数达到样本总数即可。
实验结果如下图，红点是负类样本点，绿点是正类样本点：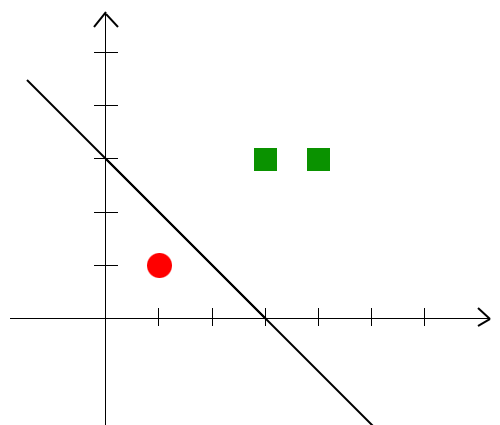
实验结果
学习到了一条直线将正类样本与负类样本分开，直线上方的是正类，下方是负类，因此对于两个测试样本的结果分别是-1和+1。
权值参数的更新过程如下图，经过了7次更新。
参数更新过程
感知机的目标仅是能够正确的将正负样本分隔开，不能保证得到最大间隔的最优超平面。

参考资料

1 《统计学习方法》by 李航

完整代码以及数据已托管至 github