在前两篇机器学习之线性回归，机器学习之线性回归II-批梯度下降与随机梯度下降中介绍了使用多种方法求解普通的线性回归问题的具体实现，属于参数学习算法(parametric learning algorithm)。本文将实现一种非参数算法(non-parametric algorithm)，即局部加权回归。

参数算法？非参算法？

在之前实现的非加权学习算法中，是一种参数学习算法，这是因为其学习了一组固定的、有限数量的参数。一旦学习好了这些参数，我们在对测试样本预测时无需再储存训练样本。
与之不同的是，局部加权回归作为一种非参学习算法，我们需要储存所有的训练样本，每次对于一个新来的测试样本，我们需要重新学习参数。

局部加权回归

核心思想

当数据实际上就是位于一条直线时，使用普通的线性回归学习算法就可以很好的解决问题，但如果数据本身是一个曲线时，线性回归的效果就并不好。这时一种方法是增加一些多次项，如：$y=\theta_0+\theta_1x+\theta_2x^2$ , 但是这样容易带来过拟合问题。另一种方法是使用局部加权回归，如果我们把整个曲线当作一小段一小段的直线来组成的话，每次预测一个新的测试样本就使用距离新样本“最近”的训练样本形成的直线来预测。

如何实现

线性回归中，我们定义了损失函数：
$$
J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})^2
$$
其中 $h(x)$ 是对样本 $x$ 的估计，表示预测的值，$x^{(i)}$ 是第 $i$ 个训练样本的特征向量，$h(x)$ 的形式如下:
$$
h(x)=\theta_0x_0+\theta_1x_1+\theta_2x_2+…+\theta_nx_n={\theta}^{T}x
$$
这里，在局部加权回归中，我们同样要定义一个损失函数，我们要为每一个训练样本增加一个不同的权重，距离测试样本近的点的权重大，反之权重小。损失函数定义如下：
$$
J(\theta)=\frac{1}{2}\sum_{i=1}^{m}w^{(i)}(h(x^{(i)})-y^{(i)})^2
$$
其中 $w^{(i)}$ 就是对应于第 $i$ 的训练样本的权重，$w^{(i)}$ 定义如下：
$$
w^{(i)}=exp(-\frac{(x^{(i)}-x)^T(x^{(i)}-x)}{2\tau^2})
$$
其中 $x$ 是测试样本的特征向量，$\tau$ 是波长参数，控制权重 $w^{(i)}$ 以多快得速率随着训练样本与测试样本的距离增大而减小。
我们用 $J(\theta)$ 对 $\theta_j$ 求偏导得到 $\theta_j$ 的更新公式为
$$
\theta_j=\theta_j-\alpha\sum_{i=1}^{m}w^{(i)}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}
$$

具体实现

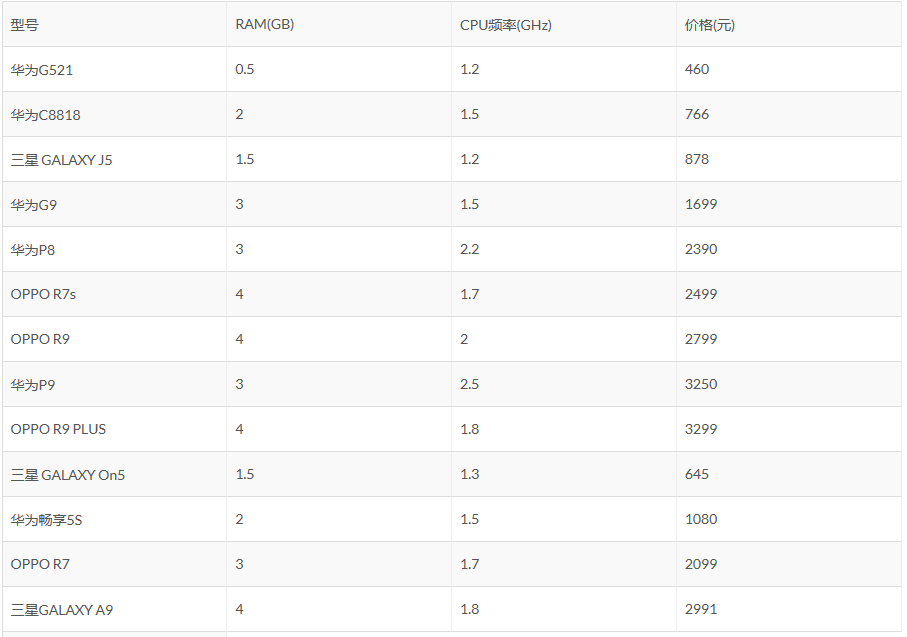
同样使用上两篇使用的案例。下表是一些手机价格的数据，我们用RAM和CPU频率作为特征，学得一个线性模型，来预测只给定RAM和CPU频率的新的手机的价格。使用前9条数据作为训练集，后4条数据作为测试集。

给出代码实现：

load data;
epsilon = 0.001; %收敛阈值
alpha = 0.005; %学习率
tau = 0.5;    %波长参数
testNum = size(test_feature, 1); %测试样本个数
n = size(X,2); %特征数+1
m = size(X,1); %训练样本个数
w = zeros(m,1); %权值
for(i = 1:testNum)
    %根据当前测试样本重新计算权值
    for(j = 1:m)
        w(j) = exp(-(X(j,:)-test_feature(i,:))*(X(j,:)-test_feature(i,:))'/(2*tao*tao));
    end;
    %求解参数theta
    theta = zeros(n,1);
    theta_new = zeros(n,1);
    while 1
        for(j = 1:n)
            theta_new(j) = theta(j);
            for(k = 1:m)
                theta_new(j) = theta_new(j) - alpha * w(k) * (X(k, :) * theta - Y(k, :))*X(k, j);
            end;
        end;
        if norm(theta_new-theta) < epsilon
            theta = theta_new;
            break;
        else
            theta = theta_new;
        end;
    end;
    predict(i) = test_feature(i,:)*theta;
end;

可以看到，对于每个测试样本，我们先计算出对应的每个训练样本的权重，然后使用批梯度下降法学习参数 $\theta$ ，最后使用这组参数预测该样本。其中tau就是上文中的 $\tau$ 。
最后给出实验结果，见下图。

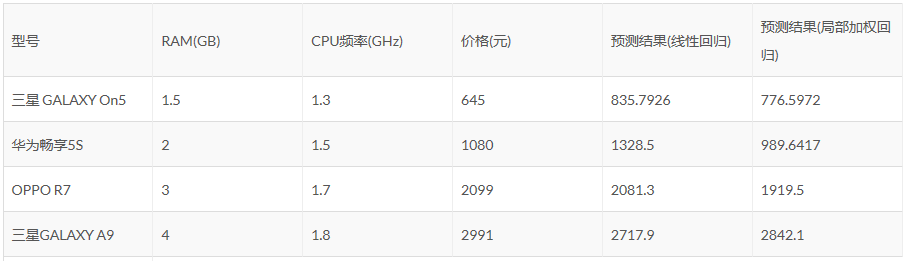
可以看到，使用局部加权回归的结果好于使用普通的线性回归的结果。但 no free lunch，结果更好的代价是付出了更多的计算时间。

参考资料

1 斯坦福机器学习公开课及其课程笔记 by Andrew Ng

完整代码以及数据已托管至 github