符号解释

训练样例 $(x, y)$
输入变量/特征 $x$ PS: $n+1$行，$1$列
输出变量/目标变量 $y$
训练样例总数 $m$
特征维度 $n$
第 $i$ 个训练样例 $(x^{(i)}, y^{(i)})$
所有训练样例的输入变量组成的矩阵 $X$ PS: $m$行，$n+1$列，每行是$(x^{(i)})^T$
所有训练样例的输出变量组成的矩阵 $Y$ PS: $m$行，$1$列

什么是线性回归

下表是某地区房屋的面积及其价格的一些数据。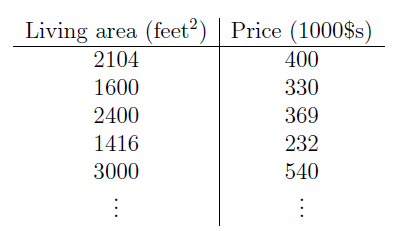

我们对这些数据进行描点画图，得到下图，线性回归就是要在图上找到一条最佳的直线来拟合价格与面积的关系。这个例子中仅包含一个特征即房屋面积。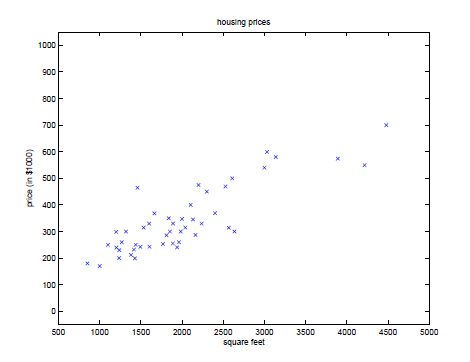

形式化来讲，给定数据集 $D = {(x_1,y_1),(x_2,y_2),…,(x_m,y_m)}$, 其中每个 $x_i$ 有 $n$ 个特征，线性回归试图学得一个线性模型，对于新来的测试集中的一个样例 $x$ ，能够输出一个尽可能准确的实数值 $y$ 。这个线性模型可以表示为
$$
h(x)=\theta_0+\theta_1x_1+\theta_2x_2+…+\theta_nx_n
$$
通常定义 $x_0=1$ ,从而上式可以变为
$$
h(x)=\theta_0x_0+\theta_1x_1+\theta_2x_2+…+\theta_nx_n={\theta}^{T}x
$$
那么如何来衡量得到的模型的好坏呢？
我们定义损失函数（cost function）
$$
J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})^2
$$
显然，预测的越准确会使得损失函数越小。由于 $J(\theta)$ 是一个二次函数的形式，其局部最优就是全局最优，可以通过对 $J(\theta)$ 求导求取其最小。

怎么用线性回归

1 梯度下降法
一方面可以通过求$J(\theta)$对每个$\theta_j$的偏导从而用梯度下降法
$$
\frac{\partial}{\partial\theta_j}J(\theta)=\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}
$$
因此可以得到梯度下降法参数更新公式
$$
\theta_j=\theta_j-\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}
$$
只要在收敛前不断迭代 $\theta$ 的值就可以使损失函数不断降低。
2 公式求解
另一方面可以直接求出 $\theta$ 的闭式解
$J(\theta)$ 可以进一步表示如下：
$$
J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})^2=\frac{1}{2}(X\theta-Y)^T(X\theta-Y)
$$
那么则有
$$
\nabla_{\theta}J(\theta)=\nabla_\theta\frac{1}{2}(X\theta-Y)^T(X\theta-Y)=X^TX\theta-X^TY
$$
为了最小化 $J(\theta)$ , 令其导数为 $\vec0$ , 从而得到参数的闭式解 $\theta=(X^TX)^{-1}X^TY$ 。详细推导过程见吴文达机器学习公开课笔记。

具体怎么用

看一个具体的例子。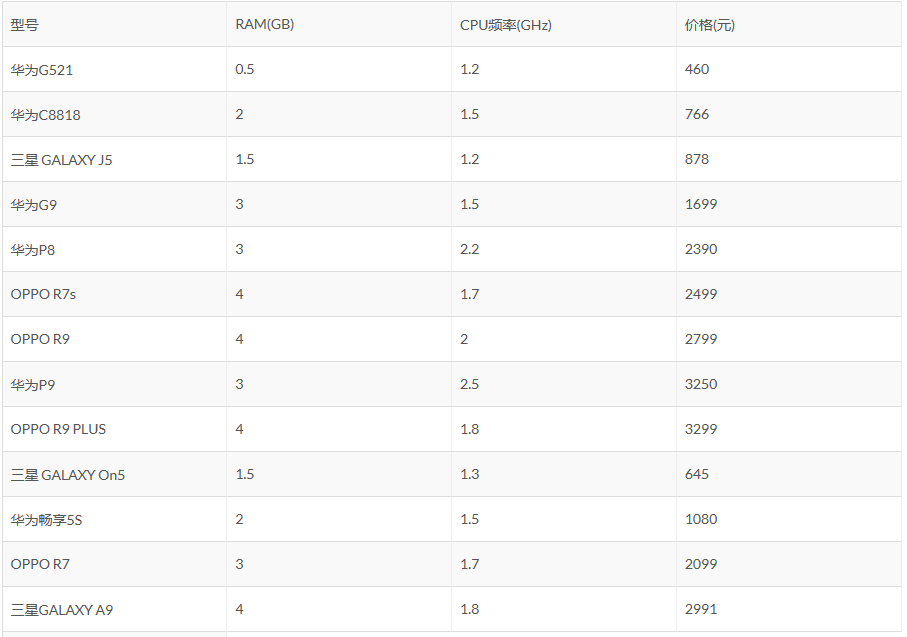

上表是我收集的一些手机数据，现在让你用RAM和CPU频率作为特征，学得一个线性模型，得到该手机的价格。现在使用前9条数据作为训练集，后4条数据作为测试集，这个线性模型该怎么学得呢？
首先将这些数据以合适的结构放到txt文件中方便导入matlab，$X$的第一列加了一排1，我直接加在文件中了，也可用代码加。然后使用上述两种思路分别实现。

使用公式求解

前面已经推导出了公式，这里给出代码。

clc;  %清屏
clear;  %清变量
load data; %导入X,Y,test_feature
theta=inv(X'*X)*X'*Y; %闭式解计算公式
predict=test_feature*theta; %对测试集预测
%以下代码用于画图，绘制的是决策面，描得点是训练集的数据
x=0:0.1:5;
y=0:0.1:5;
[x y]=meshgrid(x,y);
z=theta(1)+theta(2)*x+theta(3)*y;
surf(x,y,z);
hold on;
scatter3(X(:,1), X(:,2), Y);
xLabel('RAM/GB');
yLabel('CPU频率/GHz');

下面给出从两个角度看的结果图。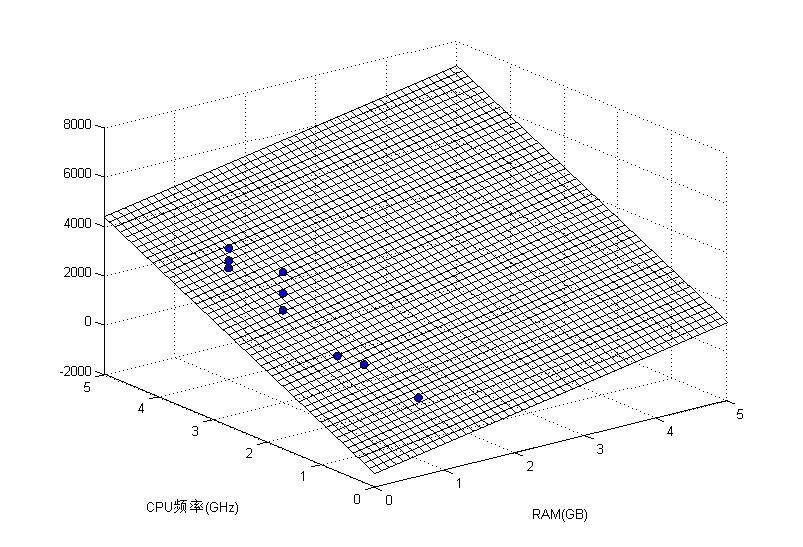

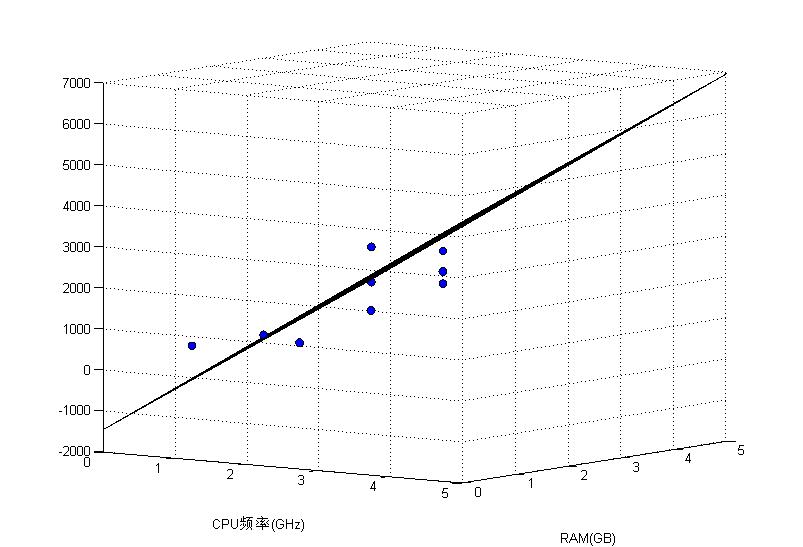
然后给出测试结果与真实标记的对比。可以看到结果还不错。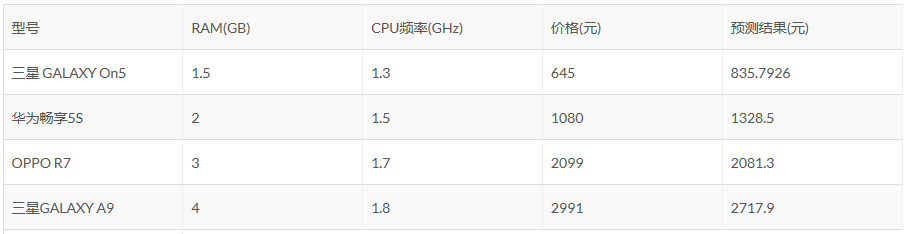

使用梯度下降方法

这里同样给出代码。

clc;  %清屏
clear;  %清变量
load data; %导入X,Y,test_feature
epsilon = 0.0001; %收敛阈值
alpha = 0.0005; %学习率
theta = zeros(size(X,2),1); 
k = 1;
figure(1);
while 1
    J(k) = 1/2 * (norm(X*theta - Y))^2;
    theta_new = theta - alpha*(X'*X*theta - X'*Y);
    fprintf('The %dth iteration, J = %f \n', k, J(k));
    if norm(theta_new-theta) < epsilon
        theta = theta_new;
        break;
    else
        theta = theta_new;
        k = k + 1;
    end
end
% 绘制损失函数变化图
plot(J);
predict=test_feature*theta;
% 以下代码使用公式求解，以比较两种方法的结果
theta_direct = inv(X'*X)*X'*Y;
predict_direct = test_feature*theta_direct;

先解释一下这行代码 theta_new = theta - alpha*(X'*X*theta - X'*Y); ，前面分析中给出的是参数向量的每一维更新的函数，这里以矩阵的形式更新，是等价的，在闭式解的推导过程中$\nabla_{\theta}J(\theta)=X^TX\theta-X^TY$，实际上也证明了这行代码的正确性。另外值得一提的是，这里采用的实际上是批梯度下降法，也就是说每次更新参数需要使用到全部数据集的数据。
然后下面给出$J(\theta)$的变化图。

然后给出上述两种方法最后得出的参数以及预测结果的对比，带_direct后缀的表示使用闭式解直接计算的，否则是梯度下降法的结果。可以看到，两者非常相近，进一步减小收敛的阈值，可以进一步让梯度下降法的结果逼近闭式解。

公式求解与梯度下降求解线性回归的对比

那么究竟什么时候使用公式求解？什么时候使用梯度下降法呢？这要依情况而定，我们来看一下二者各有何优劣。
公式求解非常精准，不需要调参，但由于要计算矩阵的逆，时间复杂度是$O(n^3)$；
梯度下降法可以更快的得到结果，但是需要调参，即收敛阈值和学习率需要手动调整。
这个问题中若采用前者，要求的矩阵的逆的矩阵是 $n+1$ 阶的方阵，也就是说当特征的维度特别大时，前者的时间复杂度将带来过长的计算时间，而维度小时毫无疑问用闭式解求取最好。具体问题中选哪个取决于在你能容忍的时间范围内你的机器上能计算出矩阵的逆的矩阵的最大阶数。

参考资料

1 斯坦福机器学习公开课及其课程笔记 by Andrew Ng
2 《机器学习》by 周志华