数据结构之线段树

发布于   |   分类于   |     |   阅读次数

什么是线段树

线段树是一种二叉搜索树，它将一个区间划分成一系列单元区间，每个单元区间对应线段树中的一个叶节点，见下图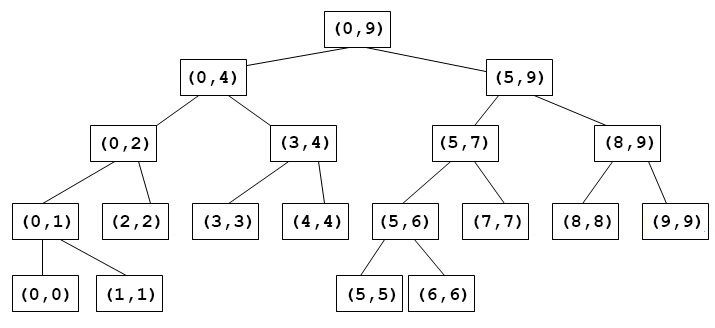
线段树
上图中每个节点中的两个值形成一个区间，(start, end)二元组，
若一个节点的start!=end，说明该节点具有孩子节点，左孩子的区间为(start, (start+end)/2)，右孩子的区间为 ((start+end)/2+1, end)
使用线段树可以快速的查找某一个索引或某个索引的区间，时间复杂度为O(logn），空间复杂度为O(n)
假设每个线段树的节点包含5个字段，start与end表示区间，left与right分别是左右孩子节点指针，value保存该节点维护的值
对于不同的问题，value可以存储不同含义的值，例如

1 区间最小数问题，value保存数组在该区间的最小数

2 区间求和问题，value保存数组在该区间的所有数之和

如何实现线段树

下面以区间求和问题为例，介绍线段树使用
问题描述如下：
实现两个方法 query(start, end) 和 modify(index, value):
对于 query(start, end), 返回数组中下标 start 到 end 的 和。
对于 modify(index, value), 修改数组中下标为 index 上的数为 value
样例
给定数组 A = [1,2,7,8,5]
query(0, 2), 返回 10
modify(0, 4), 将 A[0] 修改为 4
query(0, 1), 返回 6
modify(2, 1), 将 A[2] 修改为 1
query(2, 4), 返回 14

线段树节点Node

1
2
3
4
5
6
7
class Node{
public:
    int start, end;
    long long value;
    Node *left, *right;
    Node(int start, int end, int value):start(start),end(end),value(value),left(NULL),right(NULL){}
};

线段树SegmentTree

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
class SegmentTree {
public:
    SegmentTree(vector<int> A) {
        if(A.size()>0){
            root = build(0, A.size()-1, A);
        }
    }
    ~SegmentTree(){
        clear(root);
    }
    long long query(int start, int end) {
        return query(root, start, end);
    }
    void modify(int index, int value) {
        modify(root, index, value);
    }
private:
    Node* root;
    Node* build(int start, int end, vector<int> &A){
        //若是叶子节点，无左右孩子，值即为该索引数组的值
        if(start == end){
            return new Node(start, end, A[start]);
        }
        Node* cur = new Node(start, end, 0);
        int mid = start + ((end-start)>>1);
        cur->left = build(start, mid, A); //构造左子树
        cur->right = build(mid+1, end, A); //构造右子树
        cur->value = cur->left->value+cur->right->value; //更新该区间和为左右子树值之和
        return cur;
    }
    long long query(Node* cur, int start, int end){
        //查询与该区间完全吻合直接返回
        if(start == cur->start && end == cur->end){
            return cur->value;
        }
        int mid = cur->start + ((cur->end-cur->start)>>1);
        if(start > mid){          //查询位于右子树，仅在右子树查即可
            return query(cur->right, start, end);
        }else if(end < mid+1){    //查询位于左子树，仅在左子树查即可
            return query(cur->left, start, end);
        }else{                      //查询横跨左右子树，查询出两个子树的部分求和即可
            return query(cur->left, start, mid) + query(cur->right, mid+1, end);
        }
    }
    void modify(Node* cur, int index, int value){
        //该节点是叶子节点且是要修改的索引，则修改该节点value
        if(cur->start == index && cur->end == index){
            cur->value = value;
            return;
        }
        int mid = cur->start + ((cur->end-cur->start)>>1);
        if(index > mid){           //要修改的索引位于右子树
            modify(cur->right, index, value);
        }else{                       //要修改的索引位于左子树
            modify(cur->left, index, value);
        }
        //修改parent节点值
        cur->value = cur->left->value + cur->right->value;
    }
    //释放空间
    void clear(Node* cur){
        if(!cur) return;
        if(cur->start == cur->end){
            delete cur;
            return;
        }
        clear(cur->left);
        clear(cur->right);
        delete cur;
    }
};